5年生から始める中学受験　出るとこだけ学習するコツ

食塩水の問題は、いくらでも複雑な問題が作れるが、基本の解法はビーカー図と面積図しかないので、これをどううまく使うかが重要になってくる。

 

そして5年生の半ば以降に学習する「比」が使えると、簡単に解ける問題も出てきて、合否の分かれ目になったりする。

 

たとえば、つるかめ算でも解けるし、面積図でも解けるし、比を使っても解けるような問題があると、つるかめ算が一番時間がかかり、比を使った解法が一番楽に解けたりするのだ。

 

比を使った解法は、計算は楽だけれど、考え違いしやすいので、諸刃の剣のような解き方になる場合もある。

 

だから何でもかんでも比で解こうとすると大失敗することもよくあるが、すぐに分かるような問題であればさっさと解いて、他の問題を解く時間に回したいところだね。

面積図と比を使って解く問題

この問題は、食塩水が2つあるが、それぞれ何グラム使うかは不明。ビーカー図を描いても、普通の解き方では答えが出ない。ただ、わからない数が2つあって、合計が分かっている場合は、「つるかめ算」で解けるはず。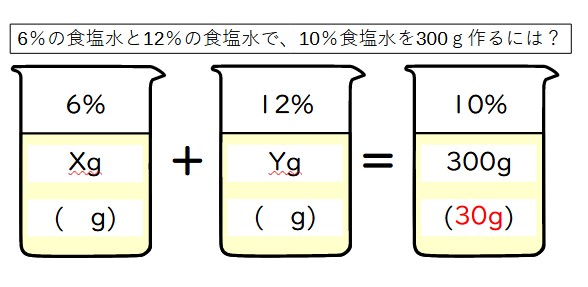

つるかめ算的な解き方

つるかめ算の考え方でこの問題を解くのであれば、まず出来上がりの食塩水に含まれる食塩の量を計算する。そうすると30グラムになるので、6％か12％の食塩水どちらかを300グラム取り、1グラムずつもう一方と置き換えていくことを考えれば良い。

 

6％で300グラムなら、含まれている塩分は18グラムで、これを1グラムだけ12％食塩水に置き換えると、（12-6）％×1グラム＝0.06グラムずつ含まれる塩分が増えていくことになる。ゴールは30グラムなので、（30-18）÷0.06＝200となり、12％食塩水を200グラム使えば良いと分かる。

 

面積図を描いて比で考える解法のほうが簡単

ただ、つるかめ算は一般的に面積図でも解けるので、面積図を描いて考えてみる。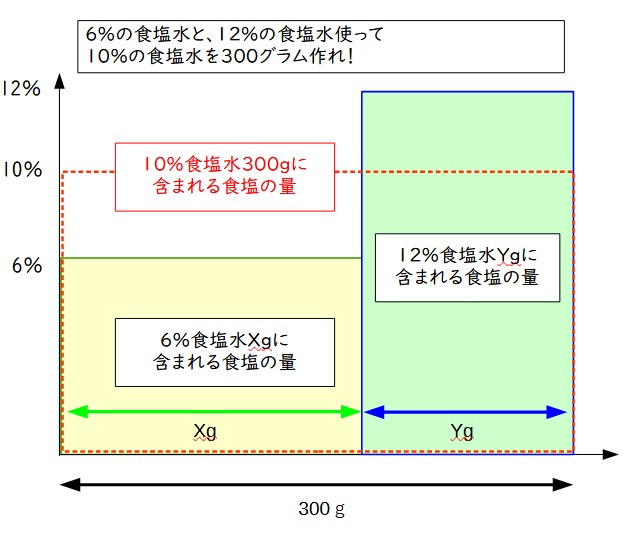

 

この面積図から、4％食塩水Xグラムに含まれる塩分と、2％食塩水Yグラムに含まれる塩分が等しくなればよいことが分かるので、X:Yは2：4であることが分かる。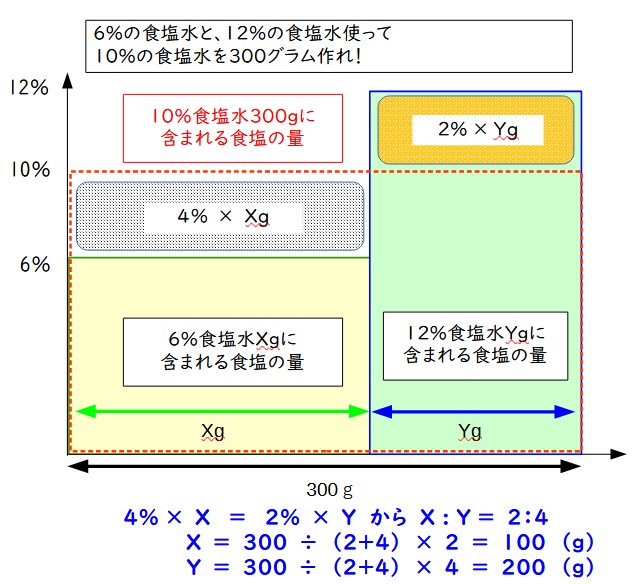

混ぜる比率が分かったので、あとは全体量をこの比率でAとBに分ければ良いだけになるわけだが、この方法は「出来上がる食塩水の量がわからなくても良い」ところに長所がある。

 

要するに、作る食塩水が100グラムだろうと300グラムだろうと、混ぜる比率は同じだから、関係ないんだよね。