5年生から始める中学受験　出るとこだけ学習するコツ

算数の問題で、実際の数量や距離、速さなどが与えられていないタイプの問題がある。

 

こういう問題は、算数が苦手な子どもにとっては、チンプンカンプンでフリーズしかねない問題だ。

 

例えばこんな感じの問題だ。

この問題の場合、家から駅までの距離も歩く速さも不明（与えられていない）から、何から始めるべきか分からずに困ってしまう子どもも多い。

距離を勝手に決めて解く方法

こういう場合、2つの解放がある。

 

一つは「駅までの距離を勝手に決める」という方法で、たとえば20と12の最小公倍数の<60>を距離として解いてみる。

 

距離を60とすれば、走る速さは60÷12＝5となり、歩く速さは60÷20＝3となるので、6分間走ると30進むことになる。

 

残りは60-30＝30になるので、歩く速さ3で割ると、残りにかかった時間が30÷3＝10とわかる。

 

初めに6分走っているので、駅につくのは6＋10＝16分後で8時16分に駅に着くとわかる。

 

この場合、駅までの距離を「１」に決めても普通に計算できる。

 

距離を「１」とした場合、走る速さは「1/12」で歩く速さは「1/20」となり、計算が分数になるのだが、分数の計算を苦手としていない子どもにとっては、別に難しい解法ではない。

 

全体を最小公倍数に決めてみるとか、「1」にしてみるというのは、仕事算でも出てきた方法だが、こういう方法に馴染めるかどうかは、子ども次第なので、どちらにしろと押し付けるのは禁物だ。

 

ただ最小公倍数に決めるのにはコツが要る場合もあるので、とりあえず「1」に決めることにしても良いが。

速さの比で解く方法

もう一つは速さの比で解く方法で、まず最初に歩く速さと走る速さの比を求める。

 

速さの比は、同じ距離を進むのにかかった時間の逆比（ぎゃくひ）になるので、この問題の場合、20；12の逆比の3：5になる。

 

ここで、歩く速さを分速③、走る速さを分速⑤、と決めることができて、そうすると歩いて20分かかる距離は（60）と決めることができる。

速さの比で距離を決める

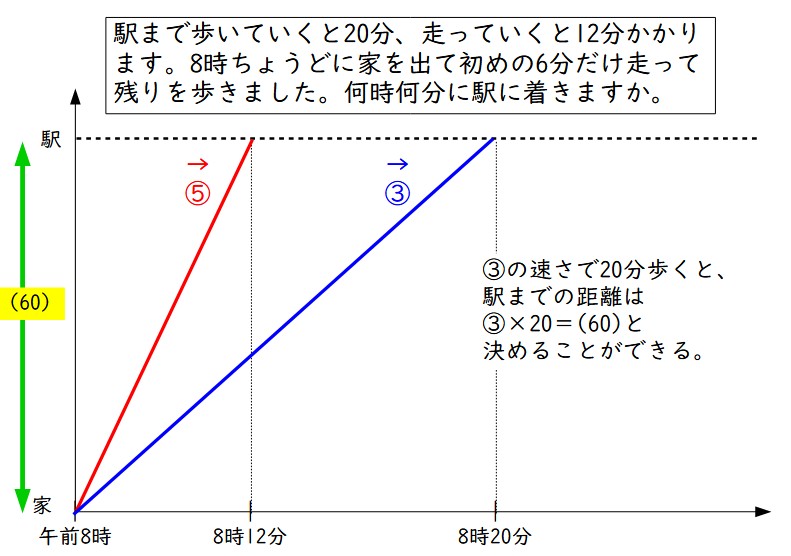
駅までの距離を(60)にするというのは、駅までの距離を最小公倍数で決めた場合と同じになっているが、距離を勝手に決めるということができない子供の場合は、速さから距離を決める方法のほうがしっくりする。

 

数学では、適当に「仮の値」を使うことが多いが、子どもによっては「勝手にそんなことしていいの？」と考えたり、「でも仮の値っていくつにすればよいの？」と迷ったりする。

 

だから速さから距離を決めるこっちの方法は、そういう子どもには適しているかもしれない。