5年生から始める中学受験　出るとこだけ学習するコツ

面積図は、グラフの図形の面積が、面積ではない数量を表す図だ。

 

例えば食塩水の問題であれば、縦軸に濃度（こさ）をとり、横軸に重量（グラム）をとった面積図を描く。

 

ということで、例題を一つ挙げる。

 

通常、食塩水の問題は「ビーカー図」を描いて解けば大体解けるのだが、これは出来上がる食塩水の重量がわかっている場合だ。

 

食塩水を混ぜた結果、何グラムの食塩水が出来るのかわからない場合は、面積図を使って解く。

面積図を描く

まず、５％の食塩水が100ｇあるのだから、縦軸に５％、横軸に100ｇをとって、長方形を描く。

 

この長方形の面積（黄色の部分）が、溶けている食塩のグラム数になる（5％×100ｇ）。

 

一方、加える10％の食塩水を右隣りに描く。

 

加える量はわからないのでXｇとして描くと、10％食塩水に含まれる塩分は緑色の部分の面積となる。

 

食塩水の問題を面積図に描く（１）

 

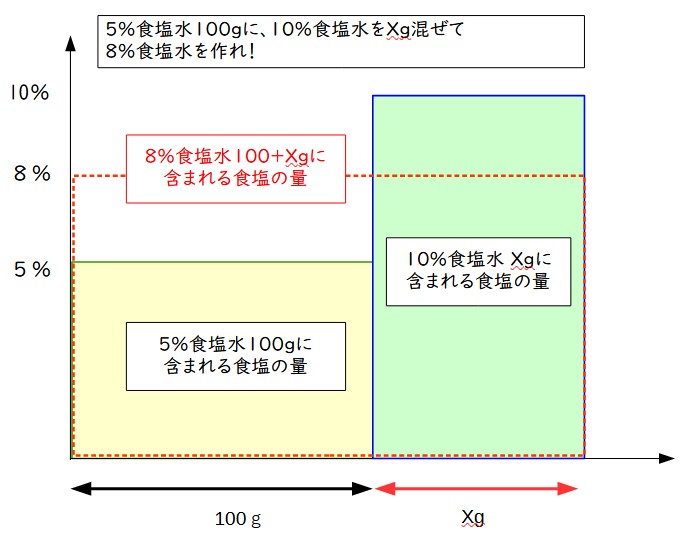
最後に、出来上がる予定の８％食塩水を描き入れるわけだが、こさは８％で重量は１００+Xgになるので、赤い点線で描いた部分になる。

 

ここまでで面積図の準備が完了だ。

出っ張った部分を、凹んだ部分に移す

８％の食塩水を作るには、どうすればよいか。

 

もとは５％の食塩水だから塩分が足りないし、１０％の食塩水は、塩分が多すぎる。

 

ということで、出っ張った部分の塩分を、凹んだ部分に移せばよいことになる。

 

食塩水の問題を面積図に描く（2）

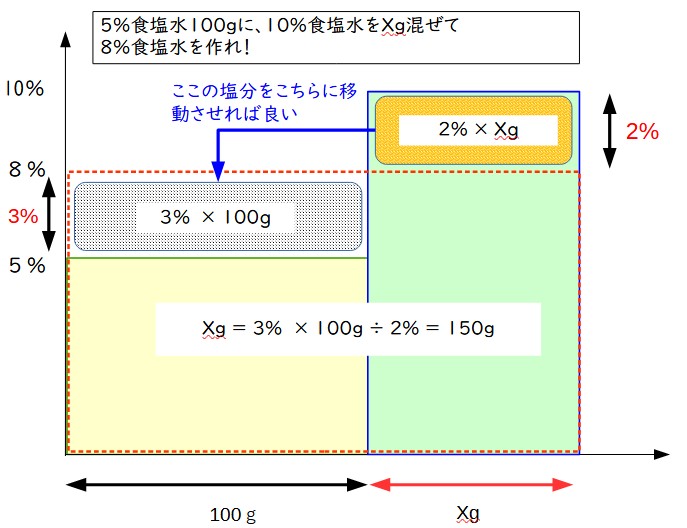
• 8％ラインを超えている部分の面積は、２％×Xｇ
• 8％ラインを下回っている部分の面積は、３％×100ｇ

だから、これが等しくなるXを求めれば良いわけで、ここからX＝150ｇと計算できる。

 

比を使って解くことも出来る

この問題は、面積図を使わなくても解ける。

 

５％の食塩水と１０％の食塩水を混ぜて８％の食塩水を作るのだから、比を使って混ぜる割合を考えても良い。

 

（8-5）：（10-8）が凸凹の部分の比になるので、その逆比の2：3の割合で混ぜれば良い。

 

ということで、100ｇ：Xg　＝　2：3　を解けば、X＝150ｇが出る。

 

ただこの比を使って解く場合も、面積図をイメージしないとわかりにくいので、一応面積図も書いた方が良い。

水を加えて濃度を下げる問題

水を加えて食塩水の濃度を下げる問題もある。

水は０％の食塩水だと考えると、含まれる食塩の量は0グラム。なので面積図では面積ナシということになるので、こういう面積図になる。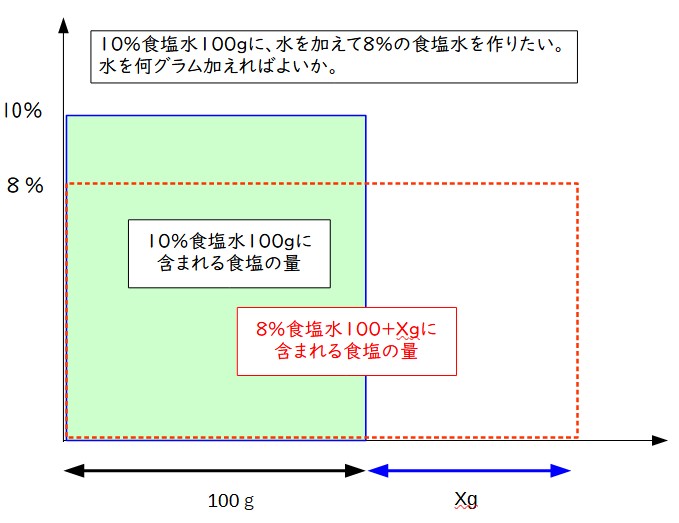

 

10％の食塩水から８％に濃さを下げるので、余分の２％分の塩分を使って、新たに８％の食塩水をXグラム作ると考えてみる。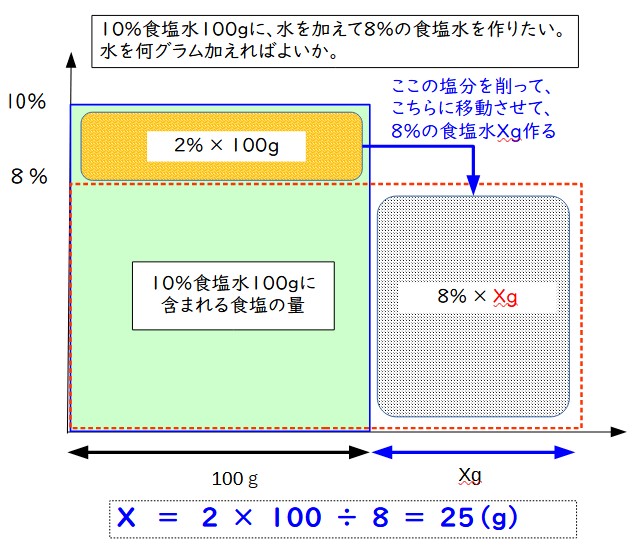

ということで、水を25グラム加えればよいということになる。