算数 三角形の面積を長方形で解く方法（うらわざ？）の解説
更新日：
前回、三角形の面積の求め方を例に出したが、ちょっとわかりにくかったかも知れないので、補足説明をしておく。
ちゃんと理屈を理解しておかないと、「き・じ・は」と同様に、生兵法となる可能性があるからだ。
（三角形の面積）＝（外枠の長方形－内枠の長方形）÷２
というやつだ。
手順としては、先ず三角形を長方形で囲む。
三角形の三つの頂点から、水平線（ヨコの線）と鉛直線（タテの線）を引くと下の図のようになる。
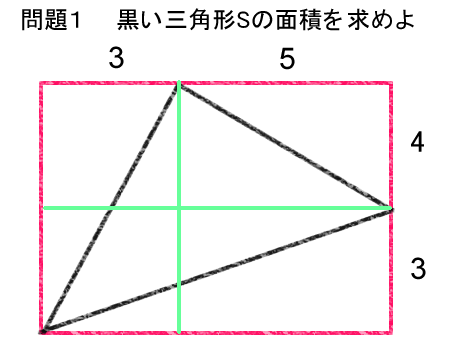
この図を描くのが、まず難しいかもしれない。
うまく描けない場合は、何にも考えずに、３つの頂点からタテの線を３本引き、ヨコの線を３本引けばいい。
で、問題は、線を引いたときにできる四つの長方形のうち、どれを計算で引くかだ。
上の図の三角形の３つの頂点のウチ、タテヨコに線が延びている頂点が１つだけある。
ここを二つに切れ目を入れて分割すると、３つの三角形ができる。
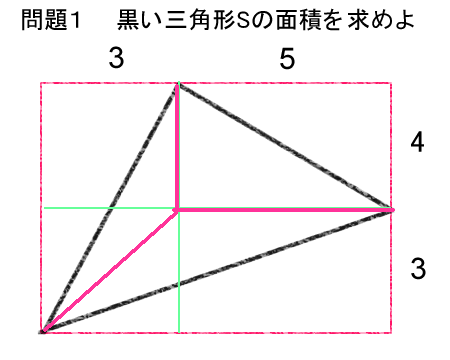
で、斜めになっている２つの三角形を、等積変形（面積が変わらないように形を変形）して、直角三角形を３つ作る。
等積変形の考え方としては、三角形の面積は、底辺と高さで決まるので、底辺をまずタテの片かヨコの片に決めて、高さが変わらないように動かせばいい。
そうすると、こんな風な面積関係になる（同じマークの付いた三角形の面積が等しい）↓
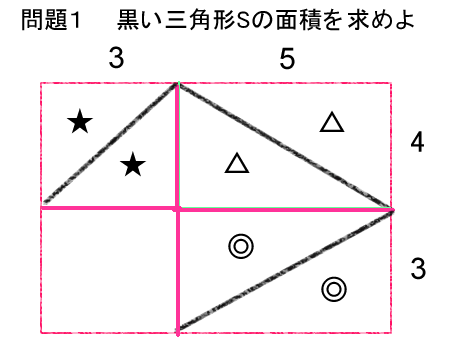
つまり、切り開いた部分の長方形以外の長方形の合計面積の半分が、元の三角形の面積になるわけだ。
この問題では、外枠が（８×７）、左下の内枠が（３×３）だから、その差が４７。
三角形の面積はその半分だから、23.5が答えと言うことになる。
こういう屈を知らずに、便利な式だけ覚えても使えない。
こういう風に変形したら、こういう理屈になると言う道筋を覚えさせるべきだろう。
でないと、結局使えない裏技になる。
