中学受験：塾からもらった問題集がわかるブログ

速さの問題は、「き・は・じ」とか「は・じ・き」で覚えている子どもは結構多い。でもこれって、式を覚えるための便法（一時しのぎの方法）であって、本質からは遠い方法だ。

だから６年生で一旦学習しても、中学生になって一次方程式の利用で速さが出てきたときに、結局また「あれってどうだったけ？」と、質問しに来る子どもが続出する。

これって、便利な方法ではあるけれど、間違えやすい方法だ。だって描き方を忘れたり、順番が違っていたら、結局間違うわけだから。しかも検証（検算）の方法がないから、確かめようがない。

これは、濃さの問題や、電流（オームの法則）の問題でも、同じコトが頻発する.

だから、この方法は根本的に、やってはいけない教え方だと、私は思う。

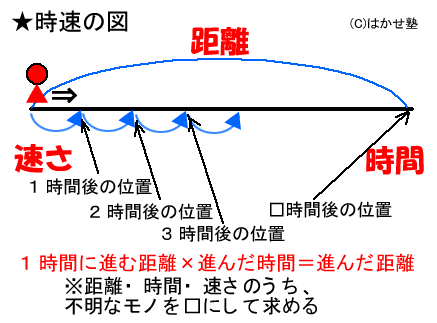
で、替わりに「時速の図」を覚えてもらう。こういう図だ↓

時速の図の使い方

時速の図は、中学になっても使えるように、中学で教える方法を元に考えた。
考え方は、ワンパターンである。学校で教えるような３つの式は覚えなくてもよい。□を使った計算ができればよい。

考え方は、

1. 時速というのは、「１時間に進む距離」のこと。


2. 同じ速さで２時間進んだら、２倍進む。３時間なら３倍進む。


3. □時間進んだら、□倍進む。

というだけである。

当たり前すぎるくらい当たり前だけど、実はこれをすんなり理解できる子どもは、案外少ない。公式主義というか何というか、便法だけ覚えてお茶を濁そうという子どもが結構多い。

図が描けないと、文章題なんか解けないので、こういう図は必ず描かせるようにする。流水算なんかだと、傾けて描くといい。

で、覚える式は１つだけ！

• １時間で進む距離（時速）　×　進んだ時間　＝　進んだ距離

で、どう問題を解くかというと、

• 時速がわからない問題なら、時速のところを□と置いて式を作って、□を求める問題に還元すればよい。


• 時間が分からない問題なら、時間のところを□と置いて式を作って、□を求める問題に還元すればよい。


• 進んだ距離を求める問題なら、進んだ距離のところが□になる。

これは、中学に上がって方程式を解くとき、□の替わりにｘやｙになるだけの方法だから、普遍性のある方法だ。